- ZÊTA (FONCTION)
- ZÊTA (FONCTION)Issues d’un calcul formel d’Euler, la «fonction zêta» de Riemann et les «fonctions L» de Dirichlet ont été jusqu’ici les outils analytiques les plus puissants pour étudier la répartition et les propriétés des nombres premiers (cf. théorie des NOMBRES - Théorie analytique des nombres). Mais ces fonctions sont elles-mêmes devenues l’objet d’études analytiques poussées, en raison de leurs propriétés très particulières qui semblent être liées aux comportements les plus cachés de la théorie des nombres et sont encore loin d’être bien comprises.Le mouvement d’idées qui tend, depuis 1920, à l’unification de la théorie des nombres et de la géométrie algébrique a conduit à définir, dans cette dernière théorie, des «fonctions zêta» et des «fonctions L» analogues aux fonctions classiques et présentant un comportement semblable. Il y a lieu de penser qu’on se trouve en présence de fragments encore mal reliés d’une vaste théorie générale, participant de l’analyse, de la théorie des groupes et de la géométrie algébrique, qui nous fera un jour pénétrer dans les recoins les plus mystérieux de la «reine des mathématiques» (C. F. Gauss), l’étude des nombres entiers.La fonction zêta de RiemannLa série:

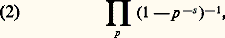 étendu aux nombres premiers p , sont tous deux absolument convergents pour s = 靖 + it de partie réelle 靖 礪 1 et représentent la même fonction analytique 﨣(s ) dans ce domaine. Le résultat fondamental de Riemann est qu’il est possible de prolonger cette fonction en une fonction méromorphe dans tout le plan, vérifiant l’équation fonctionnelle:
étendu aux nombres premiers p , sont tous deux absolument convergents pour s = 靖 + it de partie réelle 靖 礪 1 et représentent la même fonction analytique 﨣(s ) dans ce domaine. Le résultat fondamental de Riemann est qu’il est possible de prolonger cette fonction en une fonction méromorphe dans tout le plan, vérifiant l’équation fonctionnelle: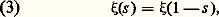 où l’on a posé:
où l’on a posé: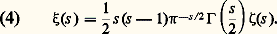 Une des démonstrations de Riemann lie la fonction zêta à une fonction thêta de Jacobi, grâce à l’expression de 臨(s ) par l’intégrale eulérienne qui donne:
Une des démonstrations de Riemann lie la fonction zêta à une fonction thêta de Jacobi, grâce à l’expression de 臨(s ) par l’intégrale eulérienne qui donne: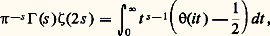 où l’on a:
où l’on a: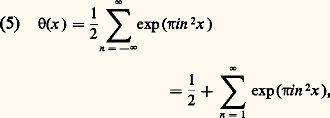

 Vu la décroissance exponentielle de (it ) 漣 1/2 à l’infini, l’intégrale dans cette formule converge pour toutes les valeurs complexes de s et ne change pas quand on remplace s par 漣 s + 1/2, d’où l’équation (3).On voit aussitôt que s = 1 est le seul pôle de 﨣(s ); il est simple et de résidu 1; les points 漣 2, 漣 4, ... sont des zéros simples de 﨣(s ), dits «triviaux». Les seuls autres zéros de 﨣(s ) sont tels que 0 諒 靖 諒 1 et Riemann a émis l’hypothèse, non encore démontrée, que tous ces zéros sont sur la droite 靖 = 1/2. On a en outre, pour le nombre N(T) des zéros contenus dans le rectangle 0 諒 靖 諒 1, 0 諒 t 諒 T, l’expression asymptotique:
Vu la décroissance exponentielle de (it ) 漣 1/2 à l’infini, l’intégrale dans cette formule converge pour toutes les valeurs complexes de s et ne change pas quand on remplace s par 漣 s + 1/2, d’où l’équation (3).On voit aussitôt que s = 1 est le seul pôle de 﨣(s ); il est simple et de résidu 1; les points 漣 2, 漣 4, ... sont des zéros simples de 﨣(s ), dits «triviaux». Les seuls autres zéros de 﨣(s ) sont tels que 0 諒 靖 諒 1 et Riemann a émis l’hypothèse, non encore démontrée, que tous ces zéros sont sur la droite 靖 = 1/2. On a en outre, pour le nombre N(T) des zéros contenus dans le rectangle 0 諒 靖 諒 1, 0 諒 t 諒 T, l’expression asymptotique: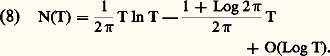 où O désigne le symbole de Landau (cf. calculs ASYMPTOTIQUES, chap. 1).Riemann avait annoncé sans démonstration qu’il y a en fait une infinité de zéros sur la droite 靖 = 1/2; ce résultat fut prouvé par G. H. Hardy en 1914 et A. Selberg a établi en 1942 qu’il y a une constante A 礪 0 telle que le nombre de zéros pour lesquels on a 靖 = 1/2 et 0 諒 t 諒 T est supérieur ou égal à AT Log T. On a calculé numériquement plus de trois millions de zéros de 﨣(s ) et on les a tous trouvés sur la droite 靖 = 1/2. Il faut noter toutefois qu’on connaît des exemples de séries de Dirichlet vérifiant des équations fonctionnelles du type (3) et ayant cependant une infinité de zéros où 靖 礪 1.Fonction zêta et fonctions L d’un corps de nombres algébriquesR. Dedekind généralisa la définition des fonctions zêta et L à un corps de nombres algébriques k , en prenant:
où O désigne le symbole de Landau (cf. calculs ASYMPTOTIQUES, chap. 1).Riemann avait annoncé sans démonstration qu’il y a en fait une infinité de zéros sur la droite 靖 = 1/2; ce résultat fut prouvé par G. H. Hardy en 1914 et A. Selberg a établi en 1942 qu’il y a une constante A 礪 0 telle que le nombre de zéros pour lesquels on a 靖 = 1/2 et 0 諒 t 諒 T est supérieur ou égal à AT Log T. On a calculé numériquement plus de trois millions de zéros de 﨣(s ) et on les a tous trouvés sur la droite 靖 = 1/2. Il faut noter toutefois qu’on connaît des exemples de séries de Dirichlet vérifiant des équations fonctionnelles du type (3) et ayant cependant une infinité de zéros où 靖 礪 1.Fonction zêta et fonctions L d’un corps de nombres algébriquesR. Dedekind généralisa la définition des fonctions zêta et L à un corps de nombres algébriques k , en prenant: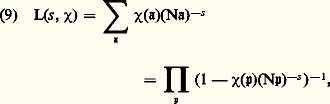 où face=F9828 a parcourt l’ensemble des idéaux entiers de k , où face=F9828 p parcourt l’ensemble des idéaux premiers, où N face=F9828 a est la norme de l’idéal face=F9828 a, c’est-à-dire le nombre d’éléments de face=F9828 o/ face=F9828 a (où face=F9828 o est l’anneau des entiers de k ) et où 﨑 est un caractère du groupe des idéaux 0 (pour 﨑 = 1, on a la fonction zêta). E. Ecke put établir que ces fonctions sont méromorphes et vérifient des équations fonctionnelles analogues à (3). Il introduisit d’autres fonctions L à l’aide de caractères plus généraux que ceux de Dedekind et put encore, au prix de calculs difficiles, prouver l’existence d’équations fonctionnelles. Dans sa thèse de 1950, J. Tate a montré comment la théorie des idèles permet une exposition simple et unifiée de tous ces travaux qui, en définitive, peuvent être fondés sur la transformation de Fourier dans le groupe des adèles de k (rappelons que la propriété (6) est une conséquence de la formule de Poisson de la théorie de Fourier classique). Dans la théorie de Tate, on considère d’une part le groupe additif k A des adèles de k et sa mesure de Haar d a, normalisée de sorte que k A/k ait pour mesure 1; il y a sur k A un caractère : k AT = R/Z tel que l’application:
où face=F9828 a parcourt l’ensemble des idéaux entiers de k , où face=F9828 p parcourt l’ensemble des idéaux premiers, où N face=F9828 a est la norme de l’idéal face=F9828 a, c’est-à-dire le nombre d’éléments de face=F9828 o/ face=F9828 a (où face=F9828 o est l’anneau des entiers de k ) et où 﨑 est un caractère du groupe des idéaux 0 (pour 﨑 = 1, on a la fonction zêta). E. Ecke put établir que ces fonctions sont méromorphes et vérifient des équations fonctionnelles analogues à (3). Il introduisit d’autres fonctions L à l’aide de caractères plus généraux que ceux de Dedekind et put encore, au prix de calculs difficiles, prouver l’existence d’équations fonctionnelles. Dans sa thèse de 1950, J. Tate a montré comment la théorie des idèles permet une exposition simple et unifiée de tous ces travaux qui, en définitive, peuvent être fondés sur la transformation de Fourier dans le groupe des adèles de k (rappelons que la propriété (6) est une conséquence de la formule de Poisson de la théorie de Fourier classique). Dans la théorie de Tate, on considère d’une part le groupe additif k A des adèles de k et sa mesure de Haar d a, normalisée de sorte que k A/k ait pour mesure 1; il y a sur k A un caractère : k AT = R/Z tel que l’application: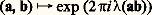 identifie k A à son dual de Pontriaguine. La transformée de Fourier d’une fonction intégrable sur k A est alors donnée par:
identifie k A à son dual de Pontriaguine. La transformée de Fourier d’une fonction intégrable sur k A est alors donnée par: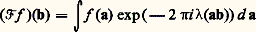 et on a la formule d’inversion habituelle (face=F0021 杻(face=F0021 杻f ))(a) = f (face=F0019 漣 a) si f est suffisamment régulière. On considère d’autre part le groupe multiplicatif des idèles k A et sa mesure de Haar d a. On appelle quasi-caractère de k A un homomorphisme continu c : k AC qui est égal à 1 sur k (de sorte qu’il s’agit en fait d’un homomorphisme dans C du groupe k A/k des classes d’idèles ). Pour un tel quasi-caractère c , il y a un nombre réel 猪 bien déterminé tel que l’on ait |c (a)|=|a| size=1猪 pour tout idèle a; on dit que c’est l’exposant de c . Pour des «fonctions poids» f : k AC satisfaisant à certaines conditions de régularité, on pose alors:
et on a la formule d’inversion habituelle (face=F0021 杻(face=F0021 杻f ))(a) = f (face=F0019 漣 a) si f est suffisamment régulière. On considère d’autre part le groupe multiplicatif des idèles k A et sa mesure de Haar d a. On appelle quasi-caractère de k A un homomorphisme continu c : k AC qui est égal à 1 sur k (de sorte qu’il s’agit en fait d’un homomorphisme dans C du groupe k A/k des classes d’idèles ). Pour un tel quasi-caractère c , il y a un nombre réel 猪 bien déterminé tel que l’on ait |c (a)|=|a| size=1猪 pour tout idèle a; on dit que c’est l’exposant de c . Pour des «fonctions poids» f : k AC satisfaisant à certaines conditions de régularité, on pose alors: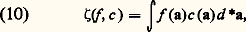 intégrale qui a un sens pour tout quasi-caractère d’exposant 礪 1.Un quasi-caractère peut toujours s’écrire (de plusieurs manières) c (a) = 﨑(a)|a|s , où 﨑 est un caractère de k A/k («Grössencharakter» dans la terminologie de Hecke) et s un nombre complexe; deux quasi-caractères correspondant au même caractère 﨑 sont dits équivalents; l’ensemble des quasi-caractères équivalents à un quasi-caractère donné a donc une structure complexe et l’on peut parler de «prolongement analytique» d’une fonction holomorphe dans un ensemble ouvert de l’ensemble des quasi-caractères.Le théorème fondamental de Tate est alors que, pour une fonction poids f donnée, la fonction c 料 﨣(f , c ), définie seulement pour les quasi-caractères d’exposant 礪 1, se prolonge en une fonction méromorphe sur l’ensemble de tous les quasi-caractères; ses seuls pôles sont le caractère trivial 﨑0 : a 料 1 et le quasi-caractère «module» N : a 料 |a|, avec des résidus respectivement égaux à 廓 練 f (0) et 漣 廓 練 杻 f (0), où 廓 est le volume de k A/k pour la mesure de Haar additive d a. Enfin, on a l’équation fonctionnelle:
intégrale qui a un sens pour tout quasi-caractère d’exposant 礪 1.Un quasi-caractère peut toujours s’écrire (de plusieurs manières) c (a) = 﨑(a)|a|s , où 﨑 est un caractère de k A/k («Grössencharakter» dans la terminologie de Hecke) et s un nombre complexe; deux quasi-caractères correspondant au même caractère 﨑 sont dits équivalents; l’ensemble des quasi-caractères équivalents à un quasi-caractère donné a donc une structure complexe et l’on peut parler de «prolongement analytique» d’une fonction holomorphe dans un ensemble ouvert de l’ensemble des quasi-caractères.Le théorème fondamental de Tate est alors que, pour une fonction poids f donnée, la fonction c 料 﨣(f , c ), définie seulement pour les quasi-caractères d’exposant 礪 1, se prolonge en une fonction méromorphe sur l’ensemble de tous les quasi-caractères; ses seuls pôles sont le caractère trivial 﨑0 : a 料 1 et le quasi-caractère «module» N : a 料 |a|, avec des résidus respectivement égaux à 廓 練 f (0) et 漣 廓 練 杻 f (0), où 廓 est le volume de k A/k pour la mesure de Haar additive d a. Enfin, on a l’équation fonctionnelle: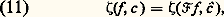 où c est le quasi-caractère c (a) = |a|(c (a))-1 (de sorte que c = c ). La démonstration est une adaptation facile de celle de Riemann rappelée plus haut; on décompose l’intégrale (10) en deux autres, étendues respectivement aux idèles tels que |a| 諒 1 et aux idèles tels que |a| 閭 1, et on ramène la première au domaine |a| 閭 1 par changement de variable et utilisation de la formule générale de Poisson de l’analyse harmonique.Pour retrouver à partir du théorème de Tate les résultats de Hecke et de Dedekind, on spécialise la fonction poids; on prend:
où c est le quasi-caractère c (a) = |a|(c (a))-1 (de sorte que c = c ). La démonstration est une adaptation facile de celle de Riemann rappelée plus haut; on décompose l’intégrale (10) en deux autres, étendues respectivement aux idèles tels que |a| 諒 1 et aux idèles tels que |a| 閭 1, et on ramène la première au domaine |a| 閭 1 par changement de variable et utilisation de la formule générale de Poisson de l’analyse harmonique.Pour retrouver à partir du théorème de Tate les résultats de Hecke et de Dedekind, on spécialise la fonction poids; on prend: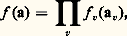 où, pour chaque place v de k , av est le composant de l’idèle a dans le corps local k v et f v une fonction convenable sur k v. D’autre part, si l’on a c (a) = 﨑(a)|a|s , on désigne par S size=1﨑 l’ensemble fini des places de k formé des places infinies et des places finies où 﨑 prend des valeurs 1 dans le groupe des unités de k v. Alors, si l’on pose:
où, pour chaque place v de k , av est le composant de l’idèle a dans le corps local k v et f v une fonction convenable sur k v. D’autre part, si l’on a c (a) = 﨑(a)|a|s , on désigne par S size=1﨑 l’ensemble fini des places de k formé des places infinies et des places finies où 﨑 prend des valeurs 1 dans le groupe des unités de k v. Alors, si l’on pose: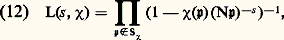 on trouve l’égalité 﨣(f , c ) = 淋(s )L(s , 﨑) où 淋(s ) est un produit de fonctions de la forme s 料 臨( 見s + 廓)m , expression dans laquelle 見 et 廓 sont des constantes complexes et m un entier rationnel, et de fonctions rationnelles par rapport à un certain nombre de puissances 福s , où les 福 sont des constantes non nulles. L’équation fonctionnelle (11) se réduit alors à l’équation de Hecke pour la fonction L.Fonctions zêta et fonctions L sur une variété algébrique définie sur un corps finiDepuis les travaux de E. Artin, on sait que tous les résultats de la théorie des nombres algébriques se transportent (avec des expressions plus simples, dues à l’absence des «places infinies») aux «corps de fonctions algébriques d’une variable sur un corps fini Fq », c’est-à-dire les extensions algébriques finies du corps des fractions rationnelles Fq (X). E. Artin lui-même avait noté, sur le cas particulier des extensions quadratiques de Fq (X), que la définition de Dedekind de la fonction zêta se généralise à un tel corps k en prenant pour face=F9828 p toutes les places de k et pour N face=F9828 p le nombre d’éléments du corps résiduel de la place face=F9828 p. La théorie de Tate s’étend également sans difficulté.Mais on peut considérer k comme le corps des fonctions rationnelles sur une courbe algébrique irréductible définie sur Fq ; ce point de vue amène à une nouvelle généralisation, en remplaçant la courbe par une variété algébrique X de dimension quelconque définie sur Fq . Pour simplifier, on supposera qu’il s’agit d’une variété affine, ensemble des points x = (x 1, ..., x m ) d’un espace Fq m , où Fq est la clôture algébrique de Fq , vérifiant un nombre fini d’équations P 見(x 1, ..., x m ) = 0, où les P 見 sont des polynômes à coefficients dans Fq . Soit face=F9828 a l’idéal de l’anneau de polynômes Fq [1, ..., Tm ] engendré par les P 見. Tout point x 捻 X définit un homomorphisme Fq [1, ..., Tm ]Fq transformant Tj en x j pour 1 諒 j 諒 m et s’annulant dans face=F9828 a; réciproquement, un tel homomorphisme correspond à un point x 捻 X et à un seul. L’image de cet homomorphisme est un corps fini, extension de Fq , ayant donc q h éléments; on pose h = deg(x ). On montre alors que le produit infini:
on trouve l’égalité 﨣(f , c ) = 淋(s )L(s , 﨑) où 淋(s ) est un produit de fonctions de la forme s 料 臨( 見s + 廓)m , expression dans laquelle 見 et 廓 sont des constantes complexes et m un entier rationnel, et de fonctions rationnelles par rapport à un certain nombre de puissances 福s , où les 福 sont des constantes non nulles. L’équation fonctionnelle (11) se réduit alors à l’équation de Hecke pour la fonction L.Fonctions zêta et fonctions L sur une variété algébrique définie sur un corps finiDepuis les travaux de E. Artin, on sait que tous les résultats de la théorie des nombres algébriques se transportent (avec des expressions plus simples, dues à l’absence des «places infinies») aux «corps de fonctions algébriques d’une variable sur un corps fini Fq », c’est-à-dire les extensions algébriques finies du corps des fractions rationnelles Fq (X). E. Artin lui-même avait noté, sur le cas particulier des extensions quadratiques de Fq (X), que la définition de Dedekind de la fonction zêta se généralise à un tel corps k en prenant pour face=F9828 p toutes les places de k et pour N face=F9828 p le nombre d’éléments du corps résiduel de la place face=F9828 p. La théorie de Tate s’étend également sans difficulté.Mais on peut considérer k comme le corps des fonctions rationnelles sur une courbe algébrique irréductible définie sur Fq ; ce point de vue amène à une nouvelle généralisation, en remplaçant la courbe par une variété algébrique X de dimension quelconque définie sur Fq . Pour simplifier, on supposera qu’il s’agit d’une variété affine, ensemble des points x = (x 1, ..., x m ) d’un espace Fq m , où Fq est la clôture algébrique de Fq , vérifiant un nombre fini d’équations P 見(x 1, ..., x m ) = 0, où les P 見 sont des polynômes à coefficients dans Fq . Soit face=F9828 a l’idéal de l’anneau de polynômes Fq [1, ..., Tm ] engendré par les P 見. Tout point x 捻 X définit un homomorphisme Fq [1, ..., Tm ]Fq transformant Tj en x j pour 1 諒 j 諒 m et s’annulant dans face=F9828 a; réciproquement, un tel homomorphisme correspond à un point x 捻 X et à un seul. L’image de cet homomorphisme est un corps fini, extension de Fq , ayant donc q h éléments; on pose h = deg(x ). On montre alors que le produit infini: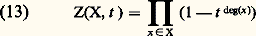
 On voit facilement que, pour tout entier n 閭 0, il n’y a qu’un nombre fini 益n de points de X tels que deg(x ) = n , et on déduit de (13) l’égalité:
On voit facilement que, pour tout entier n 閭 0, il n’y a qu’un nombre fini 益n de points de X tels que deg(x ) = n , et on déduit de (13) l’égalité: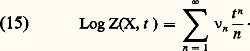 Le nombre 益n s’interprète à l’aide de l’automorphisme de Frobenius F de X, qui à tout point (x 1, ..., x m ) de X fait correspondre le point (x 1q , ..., x q m ); 益n est simplement le nombre des points de X fixes par Fn . Cette interprétation, d’abord introduite par A. Weil, est à la base de tous les résultats récents obtenus sur les fonctions zêta des variétés X.On définit de la même manière la fonction Z(X, t ) lorsque X est une variété projective sur Fq ou une variété «abstraite» au sens de A. Weil ou de J.-P. Serre. Lorsque X est une courbe projective sans singularité de genre g , F. K. Schmidt a montré en 1929 que l’on peut écrire:
Le nombre 益n s’interprète à l’aide de l’automorphisme de Frobenius F de X, qui à tout point (x 1, ..., x m ) de X fait correspondre le point (x 1q , ..., x q m ); 益n est simplement le nombre des points de X fixes par Fn . Cette interprétation, d’abord introduite par A. Weil, est à la base de tous les résultats récents obtenus sur les fonctions zêta des variétés X.On définit de la même manière la fonction Z(X, t ) lorsque X est une variété projective sur Fq ou une variété «abstraite» au sens de A. Weil ou de J.-P. Serre. Lorsque X est une courbe projective sans singularité de genre g , F. K. Schmidt a montré en 1929 que l’on peut écrire: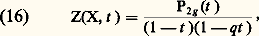
 en outre, H. Hasse pour g = 1 et A. Weil pour le cas général montrèrent que les zéros de P2g sont tels que |t | = q 1/2, ce qui correspond dans ce cas à l’«hypothèse de Riemann ». Pour X (projective ou non) de dimension quelconque, B. Dwork montra en 1960 que Z(X, t ) est encore une fonction rationnelle de t . Par exemple, si X = Fq m , on a 﨣(X, s ) = (1 漣 q m -s )-1. Grâce à l’introduction d’une notion de « cohomologie » pour les variétés sur un corps quelconque, A. Grothendieck et M. Artin ont montré que, si X est une variété projective irréductible sans singularité de dimension n sur Fq , la fonction zêta vérifie l’équation fonctionnelle généralisant (17):
en outre, H. Hasse pour g = 1 et A. Weil pour le cas général montrèrent que les zéros de P2g sont tels que |t | = q 1/2, ce qui correspond dans ce cas à l’«hypothèse de Riemann ». Pour X (projective ou non) de dimension quelconque, B. Dwork montra en 1960 que Z(X, t ) est encore une fonction rationnelle de t . Par exemple, si X = Fq m , on a 﨣(X, s ) = (1 漣 q m -s )-1. Grâce à l’introduction d’une notion de « cohomologie » pour les variétés sur un corps quelconque, A. Grothendieck et M. Artin ont montré que, si X est une variété projective irréductible sans singularité de dimension n sur Fq , la fonction zêta vérifie l’équation fonctionnelle généralisant (17):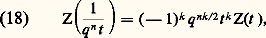 où k est la «caractéristique d’Euler-Poincaré» de X pour cette cohomologie. Mais on n’a pas encore obtenu de démonstration de l’«hypothèse de Riemann» correspondante qui serait que les zéros de Z(X, t ) soient tous sur le cercle |t | = q n /2.Suivant une idée de E. Artin, on peut aussi définir des «fonctions L» relatives à l’action d’un groupe fini G (commutatif ou non) opérant dans la variété X; on pose:
où k est la «caractéristique d’Euler-Poincaré» de X pour cette cohomologie. Mais on n’a pas encore obtenu de démonstration de l’«hypothèse de Riemann» correspondante qui serait que les zéros de Z(X, t ) soient tous sur le cercle |t | = q n /2.Suivant une idée de E. Artin, on peut aussi définir des «fonctions L» relatives à l’action d’un groupe fini G (commutatif ou non) opérant dans la variété X; on pose: pour un caractère 﨑 de G (cf. GROUPES Représentation linéaire des groupes), les nombres 益n ( 﨑) étant définis par:
pour un caractère 﨑 de G (cf. GROUPES Représentation linéaire des groupes), les nombres 益n ( 﨑) étant définis par: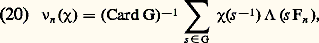 où 炙(s Fn ) est le nombre de points de X fixes par l’automorphisme s Fn . A. Grothendieck et J.-L. Verdier ont montré que ces fonctions sont encore rationnelles . Une des propriétés les plus importantes de ces fonctions est qu’elles fournissent une factorisation de la fonction zêta:
où 炙(s Fn ) est le nombre de points de X fixes par l’automorphisme s Fn . A. Grothendieck et J.-L. Verdier ont montré que ces fonctions sont encore rationnelles . Une des propriétés les plus importantes de ces fonctions est qu’elles fournissent une factorisation de la fonction zêta: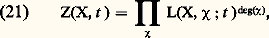 où 﨑 parcourt l’ensemble des caractères de G.Fonction zêta et fonctions L sur une variété algébrique «définie sur Z»Considérons maintenant dans l’anneau de polynômes Z[1, ..., Tm ] un idéal face=F9828 a et convenons de dire qu’il définit une «variété X sur Z» (le langage adapté à cette situation est celui des «schémas» de Grothendieck). Pour chaque nombre premier p , l’homomorphisme canonique:
où 﨑 parcourt l’ensemble des caractères de G.Fonction zêta et fonctions L sur une variété algébrique «définie sur Z»Considérons maintenant dans l’anneau de polynômes Z[1, ..., Tm ] un idéal face=F9828 a et convenons de dire qu’il définit une «variété X sur Z» (le langage adapté à cette situation est celui des «schémas» de Grothendieck). Pour chaque nombre premier p , l’homomorphisme canonique: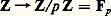 définit un homomorphisme:
définit un homomorphisme: transformant face=F9828 a en un idéal face=F9828 ap , définissant par suite une variété algébrique Xp sur Fp . On peut alors, tout au moins formellement, considérer le produit:
transformant face=F9828 a en un idéal face=F9828 ap , définissant par suite une variété algébrique Xp sur Fp . On peut alors, tout au moins formellement, considérer le produit: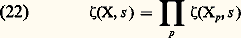 étendu à tous les nombres premiers p ; c’est la fonction zêta de Hasse-Weil . Par exemple, si l’on prend face=F9828 a = (0), on trouve 﨣(X, s ) = 﨣(m 漣 s ) où, au second membre, 﨣 est la fonction de Riemann. Si n est la dimension de X (qu’on définit ici comme le plus grand nombre tel qu’il y ait une chaîne strictement croissante face=F9828 p0 說 face=F9828 p1 說 ... 說 face=F9828 pn +1 d’idéaux premiers de Z[1, ..., Tn ] contenant face=F9828 a), on montre que le produit (22) est absolument convergent pour Re s 礪 n . On conjecture que 﨣(X, s ) peut se prolonger en une fonction méromorphe dans tout le plan et vérifiant une équation fonctionnelle analogue à (3); mais on ne sait jusqu’ici prouver cette conjecture que dans un petit nombre de cas où X est soit une courbe algébrique d’un type très particulier, soit une variété abélienne d’un type spécial, soit enfin certaines variétés fibrées ayant pour base une courbe algébrique et pour fibres des variétés abéliennes. Dans chacun de ces cas, on parvient au résultat par un calcul explicite de 﨣(X, s ) à l’aide de fonctions L de Hecke ou de Dedekind. En général, on sait seulement prolonger analytiquement 﨣(X, s ) en une fonction méromorphe dans le demi-plan Re s 礪 n 漣 1/2 et, si X 禮, le point s = n est un pôle d’ordre égal au nombre de composantes irréductibles de X de dimension n .On peut aussi considérer les fonctions L que l’on définit par une formule analogue à (22):
étendu à tous les nombres premiers p ; c’est la fonction zêta de Hasse-Weil . Par exemple, si l’on prend face=F9828 a = (0), on trouve 﨣(X, s ) = 﨣(m 漣 s ) où, au second membre, 﨣 est la fonction de Riemann. Si n est la dimension de X (qu’on définit ici comme le plus grand nombre tel qu’il y ait une chaîne strictement croissante face=F9828 p0 說 face=F9828 p1 說 ... 說 face=F9828 pn +1 d’idéaux premiers de Z[1, ..., Tn ] contenant face=F9828 a), on montre que le produit (22) est absolument convergent pour Re s 礪 n . On conjecture que 﨣(X, s ) peut se prolonger en une fonction méromorphe dans tout le plan et vérifiant une équation fonctionnelle analogue à (3); mais on ne sait jusqu’ici prouver cette conjecture que dans un petit nombre de cas où X est soit une courbe algébrique d’un type très particulier, soit une variété abélienne d’un type spécial, soit enfin certaines variétés fibrées ayant pour base une courbe algébrique et pour fibres des variétés abéliennes. Dans chacun de ces cas, on parvient au résultat par un calcul explicite de 﨣(X, s ) à l’aide de fonctions L de Hecke ou de Dedekind. En général, on sait seulement prolonger analytiquement 﨣(X, s ) en une fonction méromorphe dans le demi-plan Re s 礪 n 漣 1/2 et, si X 禮, le point s = n est un pôle d’ordre égal au nombre de composantes irréductibles de X de dimension n .On peut aussi considérer les fonctions L que l’on définit par une formule analogue à (22):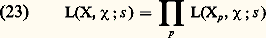 lorsque G opère sur X, c’est-à-dire lorsque G opère sur Z[1, ..., Tm ] en laissant stable l’idéal face=F9828 a; on a donc encore une factorisation:
lorsque G opère sur X, c’est-à-dire lorsque G opère sur Z[1, ..., Tm ] en laissant stable l’idéal face=F9828 a; on a donc encore une factorisation: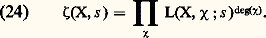 Équations fonctionnelles et représentation des groupesOn peut considérer que l’intégrale eulérienne:
Équations fonctionnelles et représentation des groupesOn peut considérer que l’intégrale eulérienne: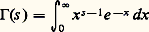 définit 臨 comme «transformée de Mellin » de e -x , la transformation de Mellin se déduisant de la transformation de Laplace bilatère (ou transformation de Fourier-Laplace) qui à une fonction f fait correspondre la fonction:
définit 臨 comme «transformée de Mellin » de e -x , la transformation de Mellin se déduisant de la transformation de Laplace bilatère (ou transformation de Fourier-Laplace) qui à une fonction f fait correspondre la fonction: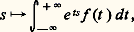 par le changement de variable x = e t dans l’intégrale; la «formule d’inversion» de la transformation de Mellin donne alors:
par le changement de variable x = e t dans l’intégrale; la «formule d’inversion» de la transformation de Mellin donne alors: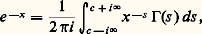 où l’intégrale est prise le long de la droite t 料 c + it dans le plan complexe, avec c 礪 0. La démonstration de l’équation fonctionnelle de 﨣(s ) par Riemann rappelée plus haut conduit à l’idée plus générale d’attacher à une série de Dirichlet:
où l’intégrale est prise le long de la droite t 料 c + it dans le plan complexe, avec c 礪 0. La démonstration de l’équation fonctionnelle de 﨣(s ) par Riemann rappelée plus haut conduit à l’idée plus générale d’attacher à une série de Dirichlet: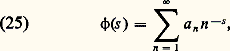 convergente dans un demi-plan, donc telle que a n = O(n c ) pour c 礪 0, la fonction f , analytique dans le demi-plan H tel que Im z 礪 0, définie par:
convergente dans un demi-plan, donc telle que a n = O(n c ) pour c 礪 0, la fonction f , analytique dans le demi-plan H tel que Im z 礪 0, définie par: pour 礪 0, de sorte que la fonction:
pour 礪 0, de sorte que la fonction: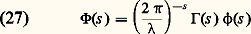 soit transformée de Mellin de f . Généralisant la méthode de Riemann, E. Hecke a remarqué que les propriétés (A) et (B) suivantes sont équivalentes.Propriété (A) . La fonction:
soit transformée de Mellin de f . Généralisant la méthode de Riemann, E. Hecke a remarqué que les propriétés (A) et (B) suivantes sont équivalentes.Propriété (A) . La fonction: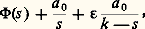 où 﨎 = size=1梁 1, est entière et bornée dans chaque «bande» |Re s | 諒 a et vérifie, pour un k 礪 0, l’équation fonctionnelle:
où 﨎 = size=1梁 1, est entière et bornée dans chaque «bande» |Re s | 諒 a et vérifie, pour un k 礪 0, l’équation fonctionnelle: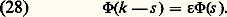 Propriété (B) . On a:
Propriété (B) . On a: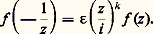 Lorsque 﨏(s ) = 﨣(2s ), on a 﨎 = 1, = 2 et k = 1/2. Une fonction analytique dans H de la forme (26), donc telle que f (z +) = f (z ), et vérifiant en outre (B) est dite forme modulaire de dimension k et de multiplicateur 﨎 pour le groupe G() engendré par les deux automorphismes z 料 z + et z 料 漣 1/z du demi-plan H. Le cas le plus important est celui où = 1, le groupe G(1) n’étant autre alors que le groupe modulaire des transformations:
Lorsque 﨏(s ) = 﨣(2s ), on a 﨎 = 1, = 2 et k = 1/2. Une fonction analytique dans H de la forme (26), donc telle que f (z +) = f (z ), et vérifiant en outre (B) est dite forme modulaire de dimension k et de multiplicateur 﨎 pour le groupe G() engendré par les deux automorphismes z 料 z + et z 料 漣 1/z du demi-plan H. Le cas le plus important est celui où = 1, le groupe G(1) n’étant autre alors que le groupe modulaire des transformations: avec a , b , c et d dans Z et avec ad 漣 bc = 1; ce groupe est le quotient de SL(2, Z) par son centre.On aperçoit donc là le début d’une étroite relation entre la théorie des représentations des groupes (du groupe GL(2) pour commencer) et les propriétés arithmétiques des courbes algébriques définies sur un corps de nombres, par le biais des fonctions zêta et L attachées à ces courbes. Cette relation est activement explorée à l’heure actuelle (A. Weil, G. Shimura, H. Jacquet et R. Langlands, P. Deligne...) et paraît pleine de promesses.
avec a , b , c et d dans Z et avec ad 漣 bc = 1; ce groupe est le quotient de SL(2, Z) par son centre.On aperçoit donc là le début d’une étroite relation entre la théorie des représentations des groupes (du groupe GL(2) pour commencer) et les propriétés arithmétiques des courbes algébriques définies sur un corps de nombres, par le biais des fonctions zêta et L attachées à ces courbes. Cette relation est activement explorée à l’heure actuelle (A. Weil, G. Shimura, H. Jacquet et R. Langlands, P. Deligne...) et paraît pleine de promesses.
Encyclopédie Universelle. 2012.
